前言

在大数据成矿预测的古今发展过程中，已经诞生了多种方法，整体上可归纳为三大类：知识驱动型、数据驱动型以及融合驱动型。

本系列文章将首先从数据驱动型方法入手展开介绍，其他类型的方法将会在后续推文中进行讨论，敬请关注微信公众号“码上地球——数学地球科学”以获取最新内容。

本文聚焦于数据驱动型的地学统计与空间分析方法，包括但不限于：

  • 证据权重法（Weights of Evidence）
  • 信息量法（Information Value Method）
  • 多准则决策分析（Multi-Criteria Decision Analysis）
  • 空间点模式分析（Spatial Point Pattern Analysis）

我们将依次介绍每种方法的原理、适用场景与案例，旨在通过回顾历史发展的脉络，帮助读者更好地理解这些方法，从而为未来成矿预测技术的创新与应用提供借鉴。

证据权重法

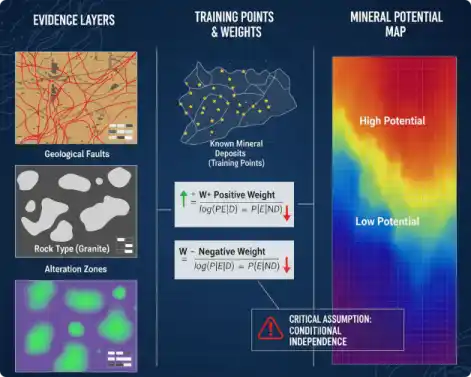
如果你的研究方向是地质大数据，那么其中一个重要的应用领域就是矿产远景制图（Mineral Prospectivity Mapping, MPM）。这一方法在文献中也常被称为矿产远景区预测图或矿产远景评价图。无论名称如何，本质上它都是一种多步骤、多准则、并依托计算机辅助的分析方法，用于在特定研究或勘查区域内，对某一类或多类矿床的存在概率进行定量评估。

在相关研究中，你会经常遇到被提及的证据权重法（Weights of Evidence, WofE）。值得注意的是，WoE并非源于地质学领域，而是一种成熟的统计学方法。它最初用于概率推理与信息融合，后来被引入并改造，以适应空间预测分析的需求，从而在矿产远景制图等地质应用中发挥出强大的优势。

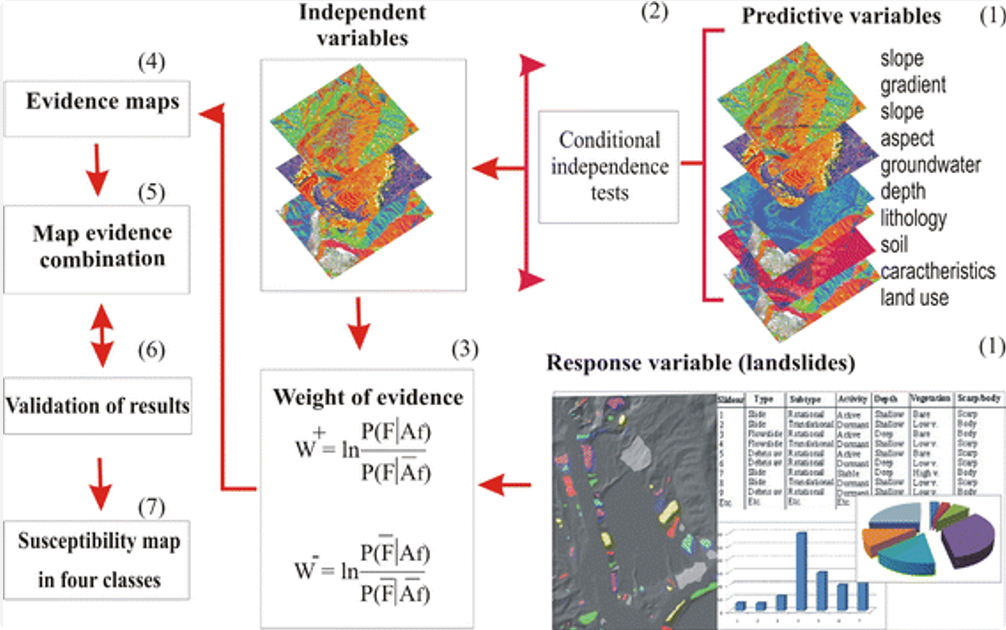
image-20250926223705437

图片来源：Armas (2012)

起源

证据权重法的最初形态诞生于医学诊断领域，其应用场景直观且易于理解 。在这个原始模型中，医生面临的“假设”是“某位病人患有 X 疾病”。支持或反对这一假设的“证据”，则是病人表现出的一系列症状（存在或缺失）。通过对大量已知病患群体的统计分析，可以量化每个症状与特定疾病之间的关联强度，并为症状的“出现”与“不出现”分别计算一个权重值 。这种方法为医学诊断提供了一种定量的、基于概率的决策支持框架，将医生的直觉判断与数据驱动的统计证据相结合 。这个早期的非空间应用，奠定了证据权重法以贝叶斯概率为核心，通过更新先验信念来评估假设的基本逻辑。

证据权重法在地学领域的应用始于20世纪80年代末，这一时期恰逢地理信息系统（GIS）技术蓬勃发展。地质学家通过将医学上的“症状”被替换为各种地质图层要素，例如特定的岩石类型、断裂构造、地球化学异常或地球物理异常；而医学上的“疾病假设”则转变为地质学上的“某个空间单元有利于形成X类型的矿床” 。将一个处理离散事件概率的非空间模型，成功地转化为一个能够整合多源空间证据、进行空间预测的强大工具。

新范式的建立

加拿大地质调查局的数学地质学家F.P. Agterberg和G.F. Bonham-Carter等人对证据权重法做出了开创性的贡献，他们是推动证据权重法在地学领域系统化和普及化的关键人物 。他们的研究不仅完善了该方法的理论框架，并将其与GIS技术紧密结合，开发了诸如Arc-WofE（ArcView GIS的扩展模块）等实用软件工具 。

在证据权重法引入之前，区域成矿预测在很大程度上依赖于地质专家的个人经验和定性判断，一种常见的做法是将多张透明地质图叠在一起，“目视解译”其要素的吻合度 。这种方法虽然蕴含了宝贵的地质知识，但过程主观，结果难以复现和量化。证据权重法作为一种数据驱动模型，通过统计计算客观地确定每个证据层对成矿的贡献权重，有效避免了证据选择和权重赋值中的主观随意性 。

实现过程

1. 数据准备

  1. 已知矿床（或目标事件）位置

    • 点数据（坐标），是模型的因变量。

  2. 潜在成矿因素（指示模式）

    • 来自地质、地球化学、地球物理、遥感等数据。
    • 转换成二元地图（presence=1 / absence=0）。
    • 常见处理方式：缓冲区（如距断层2 km内）、阈值（如元素含量>某值）、分类（岩性类型）。

  3. 空间单元划分

    • 在 GIS 中生成 unique conditions（唯一条件多边形）：每个多边形有一组唯一的指示模式状态组合。

    • 也可用规则网格（单元格）替代，但不规则多边形更精确。

    • 所谓的唯一条件多边形，其实就是根据成矿因素或者特征划分的不同特征层的“特征多边形”

image-20250926223128348

A. 显示二元证据主题和训练点的矩形区域。B. 同一区域修剪回研究区域底图，不包括点和研究区域外的区域。

图片来源：见参考内容

2. 计算证据权重

对每个指示模式 $i$：

  1. 统计：
    • $p(i|d)$：在有矿床的单元格中，该模式存在的比例。
    • $p(i|\neg d)$：在无矿床的单元格中，该模式存在的比例。
    • 同理计算 $p(\neg i|d)$、$p(\neg i|\neg d)$。
  2. 计算权重：
    • 正权重（模式存在时）： $W^+(i) = \ln \frac{p(i|d)}{p(i|\neg d)}$
    • 负权重（模式不存在时）： $W^-(i) = \ln \frac{p(\neg i|d)}{p(\neg i|\neg d)}$
  3. 对权重的解释：
    • $W^+ > 0$：模式存在增加成矿概率。
    • $W^+ < 0$：模式存在反而降低成矿概率。
    • $W^-$ 同理。

对于上面的公式过程直接看可能有点晦涩难懂，举例说明，假设 GIS 统计结果如下：

  • 有矿单元总数：68 个
  • 无矿单元总数：5000 个

在褶皱缓冲区情况下：

有矿单元中，褶皱缓冲区=1 （即在有矿的情况下，存在褶皱）的有 40 个 → $p(i|d) = 40 / 68 \approx 0.588$

无矿单元中，褶皱缓冲区=1 （即在无矿的情况下，存在褶皱） 的有 1500 个 → $p(i|\neg d) = 1500 / 5000 = 0.300$

接下来计算 W⁺：

$$W^+(褶皱缓冲区因子) = \ln \frac{0.588}{0.300} = \ln(1.96) \approx 0.673$$

解释：

  • 0.673 > 0，说明褶皱缓冲区存在时，矿床出现的可能性比无矿区域高。
  • 具体来说，概率比是 $e^{0.673} \approx 1.96$，即高出约 96%。

**接下来计算 **W⁻：

先算 p(¬i|d) 和 p(¬i|¬d)：

  • p(¬i|d) = 1 - p(i|d) = 1 - 0.588 = 0.412
  • p(¬i|¬d) = 1 - p(i|¬d) = 1 - 0.300 = 0.700

$$
W^-(2) = \ln \frac{0.412}{0.700} = \ln(0.588) \approx -0.531
$$

解释：

  • 负值表示：如果不在褶皱缓冲区内，矿床出现的可能性比无矿区域低。
  • $e^{-0.531} \approx 0.588$，即概率只有原来的 58.8%。

计算完成 W+ 和 W- 后，这两个值会在后续计算后验概率时用到：

  • 如果某个 unique condition 在褶皱缓冲区=1（即位置在褶皱缓冲区内），就加上 W⁺。
  • 如果在褶皱缓冲区=0（即位置在褶皱缓冲区外），就加上 W⁻。

3. 检验条件独立性

  • 为什么要检验：WofE 假设各模式与矿床分布条件独立，否则直接相加权重会高估或低估概率。
  • 方法：
    1. 两两（或三三）组合模式，统计它们在矿床处的联合分布。
    2. 用 G² 检验（似然比检验）或 Pearson χ² 检验比较观测频率与期望频率。
    3. 如果显著不独立：
      • 删除冗余模式。
      • 合并成新的组合模式。
      • 或用其他方法（逻辑回归、决策树）替代。

从另一个角度理解，条件独立性检验就类似于去除变量/特征的多重共线性的问题，在这里如果不独立，例如褶皱缓冲区如果和特征接触带缓冲区存在同时出现的相关性，会导致权重高估或者低估的问题。

在这个过程中，可以通过计算偏差因子可以估计忽略依赖性后导致预测概率的高估或者低估程度。

4. 计算后验概率

  1. 先验概率： $p(d) = \frac{\text{已知矿床数}}{\text{总单元格数}}$ 转成先验 logit： $\text{logit}(d) = \ln \frac{p(d)}{1-p(d)}$
  2. 后验 logit（条件独立时）： $\text{logit}(d|i_1,i_2,…,i_p) = \text{logit}(d) + \sum_{k=1}^p W(i_k)$ 其中 $W(i_k)$ 取 W⁺ 或 W⁻，取决于该模式在该单元格是否存在。
  3. 转换成后验概率： $p(d|…) = \frac{e^{\text{logit}}}{1 + e^{\text{logit}}}$

用人话说这个过程，就是：

  1. 先算全区矿床的总体概率 → 转成 logit（先验）。
  2. 每个位置看它有哪些模式存在/不存在 → 加对应的权重。
  3. 把加完的 logit 转成概率。
  4. 这个概率就是该位置的预测值。

至于为什么是这个顺序，请先简单学习贝叶斯

5. 制作预测图

  • 在 GIS 中为每个 unique condition 赋值后验概率。
  • 按概率分位数分级（如最高5%涂红），生成矿产潜力图。
image-20250926223518154

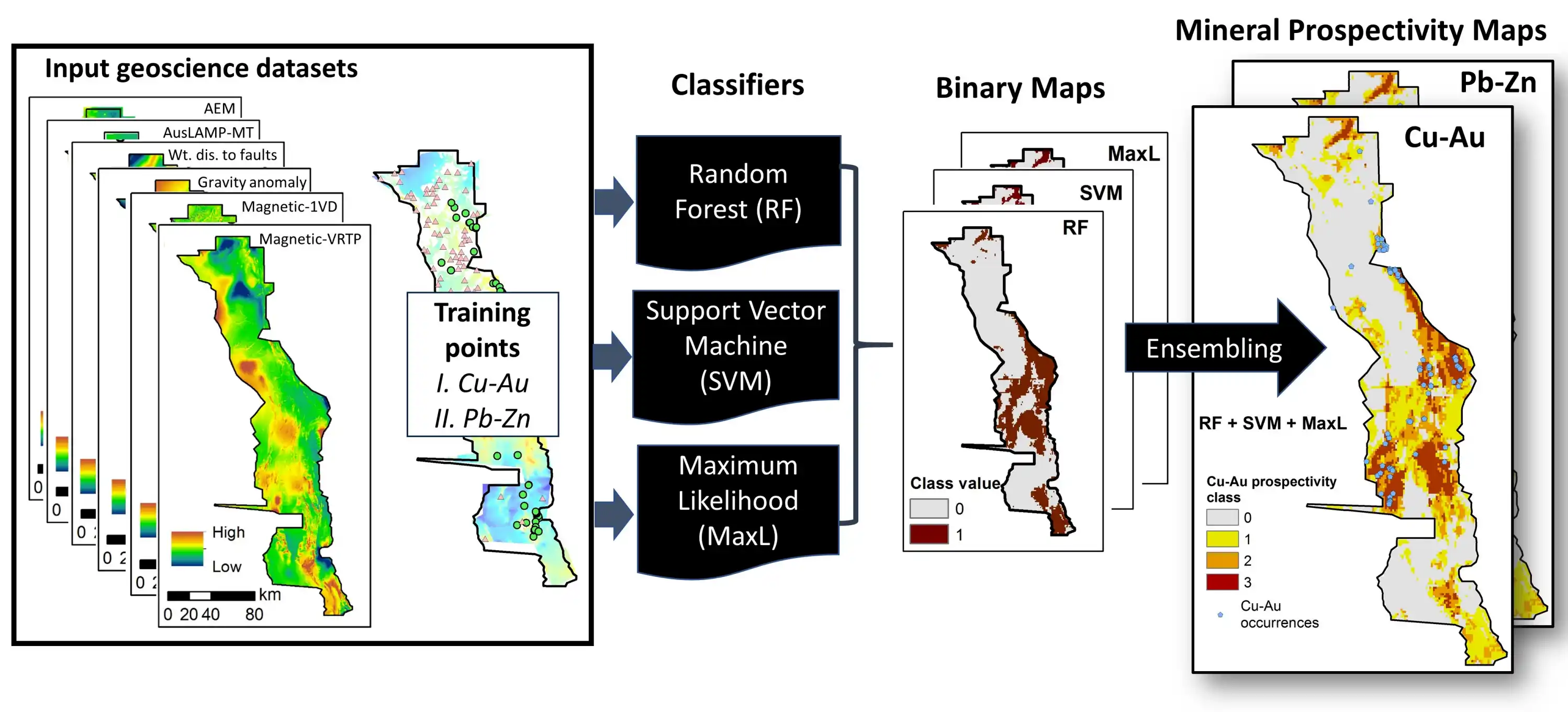
图片来源：刘杰等 (2025)

End

在了解证据权证法后你会发现，原来的思想其实和现在的思想是很像的，只是使用的算法不一样，考虑的点不一样。但是相同的是都是尝试使用数学通过建模的方式来解决现实世界的问题。

记得关注唯一微信公众号：码上地球。获取更多大数据地球科学，成矿预测相关内容。

参考内容

  • Fan, D., Cui, X. M., Yuan, D. B., Wang, J., Yang, J., Wang, S., 2011. Weight of evidence method and its applications and development. Procedia Environmental Sciences, 11, 1412-1418.
  • Agterberg, F.P. and Bonham-Carter, G.F., 1990, Deriving weights of evidence from geoscience contour maps for the prediction of discrete events: Proceedings 22nd APCOM Symposium, Berlin, Germany, v.2, p. 381-395.
  • Agterberg, F. P. (1992). Combining indicator patterns in weights of evidence modeling for resource evaluation. Nonrenewable Resources, 1(1), 39-50.
  • Agterberg, F.P., Bonham-Carter, G.F, and Wright, D.F., 1990, Statistical pattern integration for mineral exploration: In Computer applications in Resource Estimation: Predictions and Assessment for Metals and Petroleum, Eds. G. Gaal and D.F. Merriam, Pergamon, Oxford, p. 1-21.
  • Weights of Evidence Method
  • Weights of Evidence
  • 刘杰，陈力，杨徐涛.(2025). 基于MRAS证据权重法的旬北地区金矿成矿远景预测.科技与创新,(11),187-190.
  • Armaş, I. (2012). Weights of evidence method for landslide susceptibility mapping. Prahova Subcarpathians, Romania. Natural Hazards, 60(3), 937-950.