前言

这部分内容应该是和前面的经典成矿预测模型“证据权重法”放在同一个地方的，我写着写着进度快了点，给他忘了🤦‍♂️。现在慢慢补上，虽然这个系列的章节序号可能会从此有些混乱（是的，典型的自己给自己挖的“屎山”）。

好吧，现在有请我们的主角——信息量法 (Information Value Method, IVM)，它同样是矿产资源定量预测领域的经典方法之一，常与证据权重法并列，被广泛用于成矿靶区评价与优选。

起源：数学地质学派

信息量法 (Information Value Method, IVM) 作为一种定量预测工具，其“地质血统”十分清晰。信息量法最早“应用于区域矿产预测, 是由前苏联数学地质学家 E.B.维索科奥斯特罗夫斯卡娅于 1968 年首次提出，随后 N.N.恰金在 1969 年进一步完善。其设计初衷就是为了解决矿产勘查中的定量化和预测问题。 中国地质学家赵鹏大等人在 20 世纪 80 年代将其引入国内，并在矿床统计预测中取得显著成效。

范式传播：地质灾害领域的应用

尽管 IVM 起源于矿产预测，但其作为一种通用的 GIS 空间统计方法被广泛传播和应用，则主要归功于其在地质灾害（特别是滑坡易发性评价）领域的成功。大量关于滑坡灾害的研究将 IVM 的提出归功于 “Yin & Yan (1988)” 。有研究明确指出，Yin and Yan (1988) “开发了该模型并首次将其用于滑坡敏感性研究” 。

这就出现了 IVM 发展史上的“双重起源”现象：

领域先驱（矿产）： Vysokoostrovskaya & Zelenetsky 在矿产预测领域最早提出了该方法的思想。
关键传播者（地灾）： Yin & Yan (1988) 在地质灾害领域系统应用和推广了该方法，使其与 GIS 空间分析紧密结合，成为地学空间统计的“标准工具”之一。

动画演示

我非常高兴的为信息量法做了一个简短的动画演示，这是我的一次尝试，后续有足够精力的话，会依次发布到哔哩哔哩上，也请大家哔哩哔哩关注：码上地球！

核心原理与数学解构

理论基础：贝叶斯与信息论

从信息论的角度，一个地质因素 $A_j$（例如，某特定地层）对于成矿事件 $B$（有矿）所提供的“信息量” $I$，可以定义为：已知 $A_j$ 发生后，$B$ 发生的条件概率 $P(B|A_j)$ 相对于 $B$ 发生的先验概率 $P(B)$ 的变化程度。

其核心公式（常采用对数形式）为：

$$\Large I(B, A_j) = \lg \left( \frac{P(B|A_j)}{P(B)} \right)$$

公式解构如下：

$P(B)$：**先验概率 (Prior Probability)**。在整个研究区内，任意一个单元（cell）“有矿”的概率。这代表了在获得任何特定地质证据 $A_j$ 之前的“背景”成矿可能性。
$P(B|A_j)$：**条件概率 (Conditional Probability)**。在“地质因素 $A_j$”存在（例如，单元位于花岗岩缓冲区内）的条件下，该单元“有矿”的概率。
$I$：信息量。

这个公式的直观地质含义是：

若 $I > 0$，意味着 $P(B|A_j) > P(B)$。即该地质因素 $A_j$ 的存在，使得“有矿”的概率显著高于背景平均水平。这是一个“有利证据”，$A_j$ 与成矿正相关。
若 $I = 0$，意味着 $P(B|A_j) = P(B)$。该因素的存在与否，对“有矿”的概率没有影响。这是一个“无关证据”。
若 $I < 0$，意味着 $P(B|A_j) < P(B)$。该因素的存在，使得“有矿”的概率低于背景平均水平。这是一个“不利证据”，$A_j$ 与成矿负相关。

采用对数 $\lg$（或 $\ln$）具有一个关键的数学优势：它将贝叶斯框架中原本复杂的概率“乘法”关系（即多个证据的联合概率）转化为了信息量的“加法”关系。这极大地简化了计算，使得研究者可以在地理信息系统 (GIS) 中，通过简单的栅格叠加（相加），来计算每个单元所接受到的“总信息量” 。

实践中的计算公式

在实际 GIS 应用中，概率 P 通常未知，因此通过“频率”（面积或单元数量）估计。

理论公式可转化为如下实践计算公式： $$I_{A_j \to B} \approx \lg \left( \frac{N_j / S_j}{N / S} \right)$$

$S$：研究区总面积（或总单元数）[
N$：研究区内已知矿床（或矿点）的总面积（或总单元数）
$S_j$：研究区内地质因素$A_j$（如某特定地层）覆盖的面积（或单元数）
$N_j$：$S_j$区域内已知矿床（或矿点）的面积（或单元数）

实践公式经数学变换后，可揭示深层地质统计意义： $$I_{A_j \to B} \approx \lg \left( \frac{N_j / S_j}{N / S} \right)$$

$N / S$：研究区矿床（点）的全局背景密度（Global Background Density）
$N_j / S_j$：地质因素$A_j$范围内矿床（点）的局域成矿密度（Local Density）

信息量 $I$ 的本质是某地质要素内的成矿密度与全局背景成矿密度之比的对数值，可量化该地质要素 $A_j$ 对成矿的“富集”或“浓缩”能力。

总信息量与预测

信息量法的最后一步，是计算每个预测单元（栅格单元或体素）的“总信息量” $I_{total}$，即该单元上叠加的所有有利地质因素（$A_j$）的信息量之和：

$$I_{total} = \sum_{j=1}^{n} I_j$$

其中 $n$ 是影响该单元的有利地质因素的数量。总信息量越高的区域，被认为具有越高的成矿潜力。

最后，研究者可以利用受试者工作特征 (ROC) 曲线或分形分析等统计方法，对生成的总信息量图进行分析，以确定最佳的“异常阈值”（例如，信息量 > 2.6），从而客观地圈定出高潜力的勘探靶区。

信息量法的优势与局限性

核心优势

**透明性 (Transparency) / 可解释性 (Interpretability)**：

这是 IVM 相较于现代机器学习（特别是深度学习）的最大优势。IVM 是一个“白盒” (white box) 模型。与机器学习方法相比，IVM“是透明的，清楚地定义了变量之间的关系” 。地质学家可以清晰地审查每一个地质因素（如“中寒武纪天篷组”）对总预测结果贡献了多少“信息量”（正或负），这对于建立和验证地质成矿模型至关重要。
数据需求相对较低：

虽然 IVM 是数据驱动的，但“与其他方法相比，信息方法不需要大量的灾害点数据” 。它对“正样本”（已知矿床/灾害点）的依赖性很强，但对“负样本”（非矿点）的定义不那么严格。这使得 IVM 在勘探程度较低、已知矿点稀少的地区，依然能够提供有价值的初步预测。

内在局限性

条件独立性假设 (Conditional Independence Assumption)：

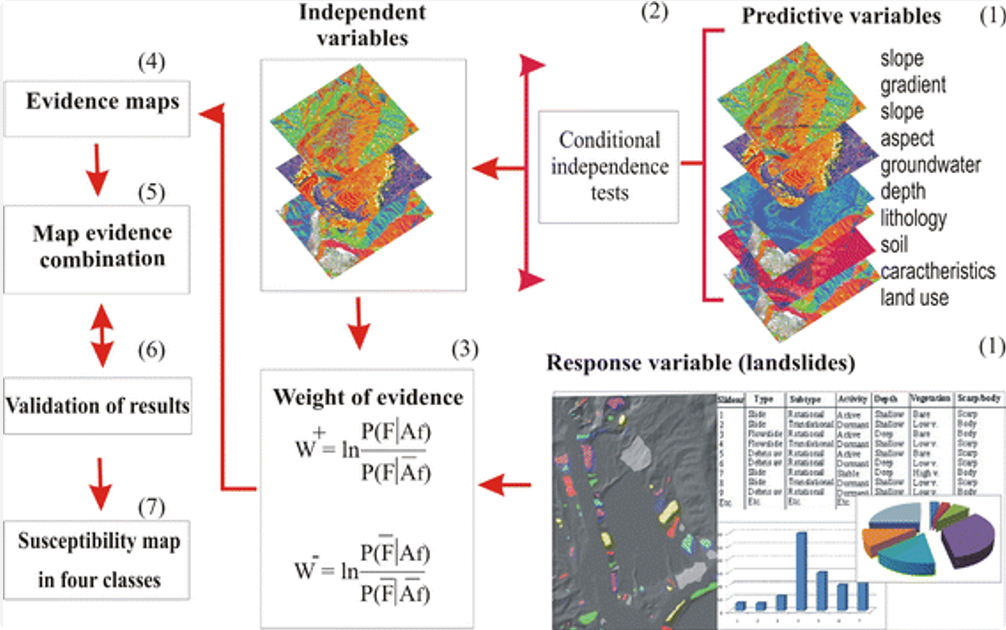
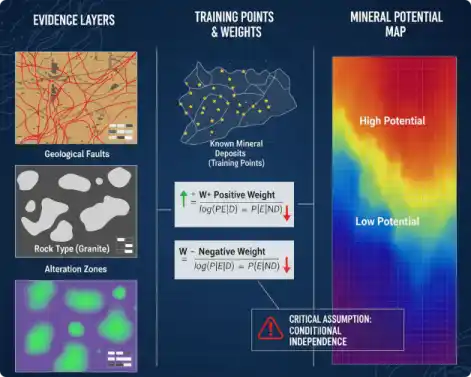
这是 IVM 在理论上最核心的缺陷。IVM 在计算总信息量时（$I_{total} = \sum I_j$），采用的是各因素信息量的简单算术叠加。这一“叠加”操作的数学前提是：所有控矿地质因素（如断层、地层、岩体）之间是“条件独立”的。然而，在地质过程中，控矿因素（如断层和岩浆活动）往往是高度相关的。IVM 是一个“双变量”(bivariate)方法，它只能分别计算 P(矿|断层) 和 P(矿|地层)，它无法捕捉到“多变量交互作用”。例如，如果成矿必须在“断层”和“特定地层”交汇处才发生（这是一个“与”逻辑，而非“加”逻辑），IVM 模型会严重低估这个交汇点的重要性，因为它只计算了断层和地层的“平均”贡献。

你会发现，它很明显，和证据权重法一样的内在缺陷
因素选择的主观性：

IVM 本身（计算信息量）是客观的统计过程，但选择哪些地质因素（图层）输入到模型中，则完全依赖于地质学家的先验知识和主观判断 。如果地质学家遗漏了一个关键的控矿因素（例如，一个未被识别的遥感异常），或者加入了一个不相关的因素，模型的结果都将是有偏的。
空间自相关性 (Spatial Autocorrelation)：

地质特征（如一个大岩体）和矿床（如一个矿田）在空间上都不是随机分布的，它们具有高度的空间聚集性（空间自相关）。IVM（以及许多用于验证它的 ROC/AUC 方法）在统计时，并未充分考虑这种空间自相关性，这可能导致其计算出的权重（信息量）被高估或低估。

结语

这是一篇填坑文章，本来应该在证据权重法之后写的，现在补上来了。值得注意的是，我在这篇文章尝试了使用动画的形式解释这个模型，如果觉得不错，后续我会慢慢把这些模型做一个动画系列专门发到哔哩哔哩上。

哦对了，下一篇文章内容应该是逻辑回归模型（可能，我打算最后把证据权重法，信息量法，逻辑回归最后总结一个表格放一起）。

科学探索永无止境，本文仅为笔者个人学习总结。因知识所限，文中若有不当之处，敬请方家斧正。

参考内容

赵鹏大.(2002).“三联式”资源定量预测与评价——数字找矿理论与实践探讨.地球科学,(05),482-489.
肖克炎,张晓华,陈郑辉,宋国耀,葛艳,刘冬林,王四龙,宁书年,曹燕.(1999).成矿预测中证据权重法与信息量法及其比较.物探化探计算技术,(03),223-226.
白万成.成矿预测中的证据权重法和信息量法的对比分析.第十二届全国数学地质与地学信息学术研讨会论文集.武警黄金指挥部;,2013:366-367.
魏冠军,党亚民,章传银,等.GIS的信息量法在澜沧老厂成矿预测中的应用[J].测绘科学,2010,35(06):217-218+246.DOI:10.16251/j.cnki.1009-2307.2010.06.081.
Tang, R.-X., Yan, E.-C., Wen, T., Yin, X.-M., & Tang, W. (2021). Comparison of Logistic Regression, Information Value, and Comprehensive Evaluating Model for Landslide Susceptibility Mapping. Sustainability, 13(7), 3803.
Wang, Q., Guo, Y., Li, W., He, J., & Wu, Z. (2019). Predictive modeling of landslide hazards in Wen County, northwestern China based on information value, weights-of-evidence, and certainty factor. Geomatics, Natural Hazards and Risk, 10(1), 820-835.
Velazco, S., Rodríguez, Á., Riascos, M., Nieto, F., & Granados, D. (2025). Evaluation of Landslide Risk Using the WoE and IV Methods: A Case Study in the Zipaquirá–Pacho Road Corridor. GeoHazards, 6(2), 27.
Ma, J., Wang, X., & Yuan, G. (2023). Evaluation of geological hazard susceptibility based on the regional division information value method. ISPRS International Journal of Geo-Information, 12(1), 17.