前言

这部分内容会比较短，主要是简单说明一下自编码器。当然，自编码器其实更多的是在地球化学异常识别的情况下更加得心应手，所以这篇文章其实和“成矿预测”稍微有点偏题，不过终归而言，它们也是异常识别的一部分。

之前提到，现代矿产勘查正在经历一场变革，从传统的经验驱动模式转向数据驱动的定量预测 。这一转变的核心驱动力在于多源地质“大数据”的爆发。然而，地质数据并非简单的“大数据”集合，其固有的复杂性对传统分析方法构成了严峻的“科学问题”：

  1. 高维性与非线性: 地球化学数据通常包含几十种元素的浓度信息 。这些元素在复杂的成矿过程中，其相互关系（如协同富集或拮抗）往往呈现高度非线性的特征 ，远非简单的线性相关所能概括。
  2. 强噪声与数据缺失: 地质勘查数据，无论是岩石、土壤还是水系沉积物样本，在采集和分析过程中不可避免地会引入噪声、异常值甚至数据缺失 。这些干扰严重掩盖了与成矿相关的真实地质信号 。
  3. 空间自相关性: 地质现象在空间上是连续的，相邻的样本点通常具有相似的地质属性 。这种空间依赖性是地质统计学的基石，但常被传统的数据挖掘算法所忽略 。
  4. 非正态分布: 元素浓度等地质变量通常不服从正态分布，而是呈现对数正态或更复杂的分布形态 ，这使得依赖正态假设的经典统计模型失效。

在此背景下，深度学习因其强大的“稳健学习和模拟能力” 而进入了地质学家的视野。 深度自编码器 (Deep Autoencoders, DAE) 作为深度学习家族中的一个关键分支 ，凭借其两大核心特性，成为解决上述“科学问题”的理想候选者：

  1. 无监督学习: DAE 不需要预先标记的“矿点”或“非矿点”数据。这在地质勘查中至关重要，因为钻探验证成本高昂，导致已知的“正样本”（矿点）极其稀少 。DAE 能够从海量的、未标记的背景数据中自行学习。
  2. 非线性特征提取: DAE 的核心能力是自动学习数据中复杂的非线性结构和有效的数据表示 。
image-20251111192304883

DAE 的引入，标志着成矿预测领域的一次范式转变：从依赖专家经验的“特征工程” 转向由模型驱动的“特征学习” ，即从原始地质数据中自动挖掘隐藏的成矿模式。

深度自编码器：非监督特征学习的理论基石

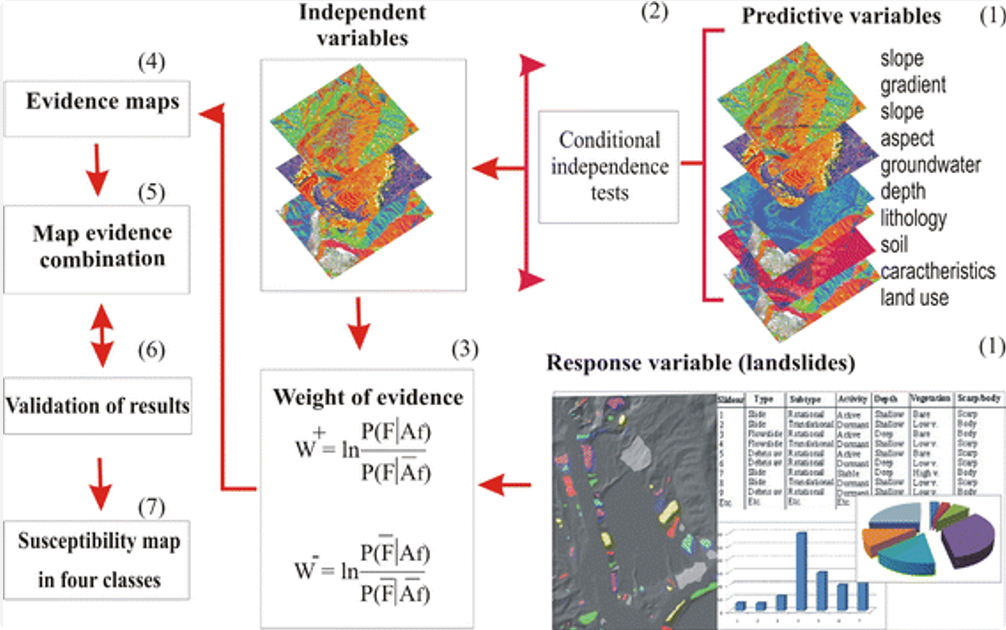
DAE 的核心架构与工作原理

深度自编码器 (DAE) 是一种无监督神经网络，其目标是学习输入数据的压缩表示（潜在特征），并利用该表示以尽可能高的保真度重建原始输入 。

其对称结构，主要由两部分组成：

  1. 编码器 (Encoder): 网络的“压缩”部分。它接收高维的输入数据（例如，一个包含30种元素浓度的地球化学样本），通过一系列神经网络层（全连接层或卷积层）将其映射到一个低维的“瓶颈层” 或“潜在空间” 。这个过程强制模型学习数据中最重要的、最本质的特征，生成一个经过压缩的特征向量 。
  2. 解码器 (Decoder): 网络的“重建”部分。它获取编码器生成的低维潜在特征，通过一系列“反向”的网络层，尝试将其“解压”并重建出与原始输入数据维度一致、表达相近的特征向量 。
  3. 重建损失: 整个网络的优化目标是最小化“重建误差” ，即原始输入数据与解码器重建数据之间的差异。这个误差通常通过均方根误差等指标来衡量。

从人话的角度来理解，就是自编码器企图用另一种方式来表示原始数据，在保持原始数据特征和另一种新的数据形式之间最小化差异的情况下。

image-20251111192754994

深度自编码器原理图

DAE 如何解决地质“科学问题”

DAE 的架构使其在解决地质数据复杂性方面具有独特的优势，尤其是为“异常检测”提供了全新的思路。

DAE 在地质学中最核心的应用范式是基于“重建误差”的异常检测 。其基本逻辑如下：

  1. 学习“背景”： 在训练过程中，DAE 接触到的是海量的地质勘查数据，其中绝大多数（例如99%以上）是无矿的“背景”样本。为了最小化总体的重建损失，DAE 会“被迫”成为一个高效的“背景重建专家”。
  2. 识别“异常”： 当一个“异常”样本（如未见过的矿化样本）被输入这个训练好的模型时，由于这个样本的模式与模型所熟知的“背景模式”截然不同，模型无法高效地重建它。
  3. 范式转变： 这导致“异常”样本会产生比“背景”样本“相对更高的重建误差” 。因此，DAE 将地质异常识别的范式从传统上“寻找高浓度值” 转变为“寻找高重建误差”——即寻找那些模型无法理解、无法重建的“独特模式”。
image-20251111193615398

这种新范式对于寻找那些被复杂背景掩盖、或元素浓度绝对值不高但“元素组合模式”独特的隐伏矿或新型矿床，具有革命性的意义。

DAE在地球科学的应用起源与模型演化

DAE 在地质学中的应用并非一蹴而就，而是从一个基础模型的引入，逐步演化为一个庞大的模型家族，以应对地质科学中日益复杂的特定挑战。

起源追溯：DAE用于地球化学异常识别的开创性研究

如果我没记错的话，深度自编码器在成矿预测领域的应用起源，一个被广泛引用的里程碑是 Xiong and Zuo (2016) （左老师团队）发表的 《Recognition of geochemical anomalies using a deep autoencoder network》 。

这个研究的核心贡献在于：

  1. 方法论建立： 明确提出利用 DAE 网络对“具有未知复杂多元概率分布”的地球化学样本群进行编码和重建。
  2. 核心发现： 论文指出，在训练过程中，那些“小概率样本”（即地质异常）对 DAE 网络的整体贡献很小。因此，训练好的模型在试图重建这些异常样本时，会自然地产生“相对更高的重建误差”。
  3. 实证验证： 该研究以中国福建西南部的 Fe 多金属矿床为例 。结果显示，通过 DAE 重建误差计算得到的“异常得分图”中，高分区域与大部分已知的Fe矿床分布高度吻合。

这项工作 成功地将 DAE 的“重建误差”这一机器学习指标与地质学上的“地球化学异常”建立了直接联系，为 DAE 在 MPM 领域的广泛应用奠定了方法论基础。

适应地质挑战：DAE“家族”的演进

基础的 DAE 解决了非线性和高维问题，但地质数据的其他独特挑战（如强噪声、空间相关性） 催生了 DAE 的多种专业化变体。 例如：

为了解决地质数据普遍存在噪声或缺失值的问题。通过降噪自编码器，接收“损坏”或“含噪声”的数据作为输入，但其重建目标是“干净”的原始数据。

为了解决基础 DAE 通常使用全连接层，它将每个地质样本视为孤立点，完全忽略了地质数据中至关重要的“空间相关性” 。 通过卷积自编码器将DAE中的全连接层替换为“卷积层和池化层” 。使 DAE 从“点”分析进化到了“面”分析，这更符合地质学的空间思维模式。

为了解决基础 DAE 的瓶颈层（潜在空间）虽然维度低，但所有神经元可能仍是“稠密”激活的，这可能导致特征冗余。稀疏自编码器在 DAE 的损失函数中加入“稀疏性惩罚”（例如L1正则化），迫使模型在瓶颈层中只激活少数最关键的神经元。 这使得SAE能够学习到数据中更具代表性、更“稀疏”的低维特征 。在成矿预测中，这有助于模型识别出最关键的少数几个成矿指示特征，实现更高效的压缩和特征表达 。

基础 DAE 提供的“重建误差”是一个确定性数值。为了解决如何科学地设置“异常”阈值这个问题。 通过变分自编码器。它不学习一个确定的潜在向量，而是学习数据在潜在空间中的“概率分布”（通常是均值和方差）。它在损失函数中引入了Kullback-Leibler (KL) 散度 来规范这个分布。 变分自编码器提供了“概率合理的方式降维”。在异常检测中，它提供的不是“重建误差”，而是“重建概率”。一个样本的重建概率越低，它就越可能是异常。这种概率度量“更具原则性和客观性，并且不需要模型特定的阈值” 。这在地质勘探这种高风险、高不确定性的决策中至关重要，并为后续的“不确定性量化” 奠定了基础。

如下表是深度自编码器 (DAE) 变体在地质数据分析中的对比：

模型变体 核心架构/技术 解决的关键地质问题 地质应用
基础 DAE 编码器-解码器，重建误差 非线性降维，高维数据 地球化学异常（背景-异常）分离
降噪 DAE 输入损坏数据，重建干净数据 数据噪声、缺失值、不完整数据 鲁棒的地球化学特征提取
卷积 CAE 卷积层/池化层 空间自相关性、空间模式 遥感图像地质填图 , 地球化学空间分布特征
稀疏 SAE 稀疏性惩罚（L1正则化） 特征冗余，提取高效/稀疏特征 稀疏低维特征提取 , 混合异常检测
变分 VAE 概率编码，KL散度，重参数化 异常阈值不确定性，数据生成 概率性异常检测 , 不确定性量化

结语

这部分只是稍微展开说一下自编码器的应用，主要是为了下一篇贯穿全部大数据成矿预测系列的内容作基础准备，下一篇大数据成矿预测系列的文章应该是当前的最后一篇，后面就不会更新的这么勤了，会更加深入的更新了。

image-20251111195810228

科学探索永无止境，本文仅为笔者个人学习总结。因知识所限，文中若有不当之处，敬请方家斧正。

参考内容

  • Xiong, Y., & Zuo, R. (2016). Recognition of geochemical anomalies using a deep autoencoder network. Computers & Geosciences, 86, 75-82.
  • Xiong, Y., & Zuo, R. (2022). Robust feature extraction for geochemical anomaly recognition using a stacked convolutional denoising autoencoder. Mathematical Geosciences, 54(3), 623-644.
  • Chen, L., Guan, Q., Feng, B., Yue, H., Wang, J., & Zhang, F. (2019). A multi-convolutional autoencoder approach to multivariate geochemical anomaly recognition. Minerals, 9(5), 270.
  • Yang, N., Zhang, Z., Yang, J., & Hong, Z. (2023). Mineralized-anomaly identification based on convolutional sparse autoencoder network and isolated forest. Natural Resources Research, 32(1), 1-18.