【6.0】支持向量机
前言
支持向量机(Support Vector Machines),简直就是 21 世纪酷刑😥
本文内容学习来源感谢:
- 《Machine Learning in Action》
- 《智能之门》
- 哔哩哔哩,维基百科等网络
前排说明:本文所有代码基于 Python 3.10 版本,理论上你的版本为 3.X 皆可运行。
基于最大间隔分隔数据
支持向量机
- 优点:泛化错误率低,计算开销不大,结果易于解释
- 缺点:对参数调节和核函数的选择敏感,原始分类器不加修改仅适用于二类问题
- 适用数据类型:数值型和标称型数据
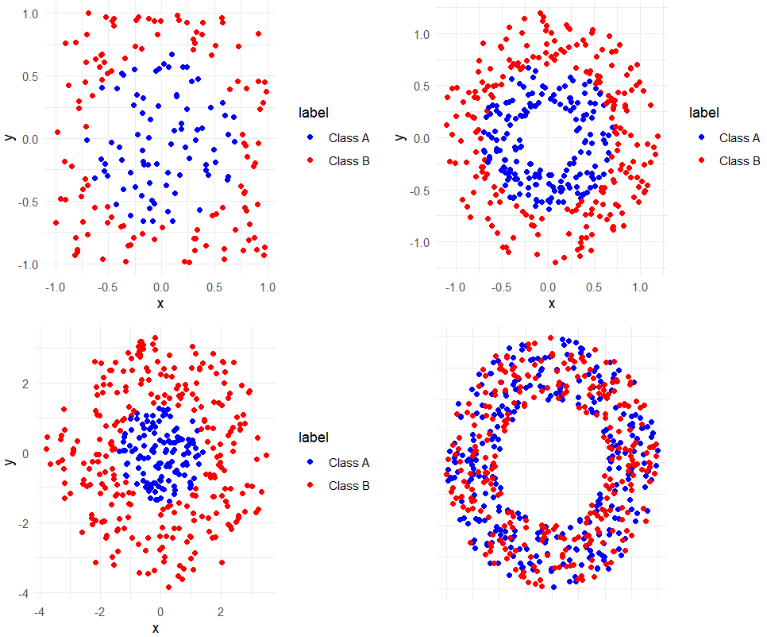
在开始说明 SVM 之前,需要先解释几个概念,考虑上图四个数据点分布图像,一个问题是:能否画出一条直线将不同类别的点区分开来?先考虑下图中的数据,它们之间已经分隔的足够开,因此可以很容易的在图中画出一条直线将两组数据分开。在这种情况下,这组数据被称为线性可分(Linearly separable)数据 。
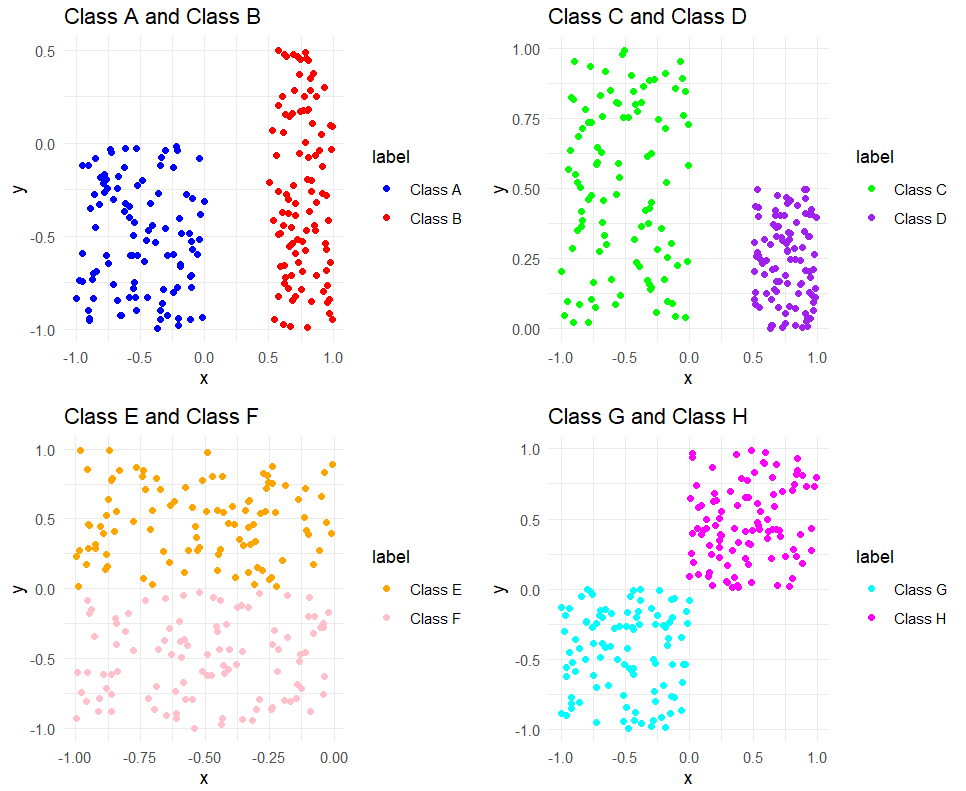
上述将数据集分割开来的直线称为分隔超平面(separating hyperplane)。在上面给出的例子中,由于数据点都在二维平面山,所以此时的分隔超平面就是一条直线。但是,如果给的数据集是三维的,那么此时用来分隔数据的就是一个平面。更高维度的依次类推。如果数据集是 1024 维度,那么就需要 1023 维度的某对象来对数据进行分隔。这个 1023 维的某对象称为超平面(hyerplane),也就是分类的决策边界。分布在超平面一侧的所有数据都属于某个类别,而分布在另一侧的所有数据都属于另一个类别。
我们希望采用这种方式来构建分类器,即如果数据点距离决策边界很远,那么最后其预测结果也就越可信。我们希望找到离分隔超平面最近的点,确保它们离分隔面的距离尽可能的远,这里点到分隔面的距离被称为间隔(margin)。我们希望间隔尽可能的大,这是因为如果我们犯错或者在有限数据上训练分类器的话,我们希望分类器尽可能的健壮1。
支持向量(support vector)就是距离分隔超平面最近的那些点。接下来要试着最大化支持向量到分隔面的距离,需要找到此问题的优化解决方法。
寻找最大间隔
如何求解数据集的最佳分割线?如下图所示。分隔超平面的形式可以写成 $\large w^Tx +b$ 。要计算点到分隔超平面的距离,就必须给出点到分隔面的法线或者垂线的长度,该值为 $\Large \frac{|w^Tx + b|}{||w||}$ 。这里的常数 $b$ 类似于 Logistic 回归中的截距 $w_0$ 。这里的向量 $w$ 和常数 $b$ 一起描述了说给数据的分割线或者超平面。
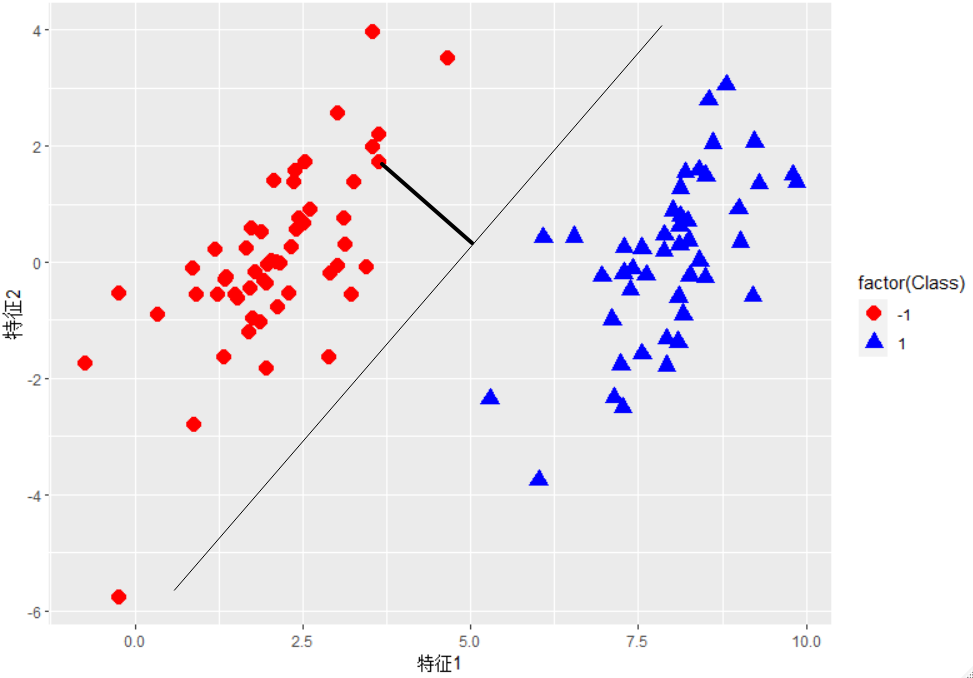
分类器求解的优化问题
前面提到了分类器,但是还没有介绍它的工作原理。理解其工作原理将有助于理解基于优化问题的分类器求解过程。输入数据给分类器会输出一个类别标签,这相当于一个类似于 Sigmoid 的函数在作用。下面将使用类似于赫维赛德阶跃函数(单位阶跃函数)的函数对 $\large w^Tx+b$ 作用得到 $f(x^Tx+b)$ ,其中当 $u<0$ 时 $f(u)$ 输出 $-1$ ,反之则输出 $+1$ 。这和前面的 Logistic 回归有所不同,那里的类别标签是 0 或 1。
这里的类别标签为什么采用 $-1$ 和 $+1$ ,而不是 0 或者 1呢?这是由于 $-1$ 和 $+1$ 仅仅相差一个符号,方便数学上处理。我们可以通过一个统一公式来表示间隔或者数据点到分割超平面的距离,同时不必要担心数据到底是属于 $-1$ 还是 $+1$ 。
当计算数据点到分隔面的距离并确定分隔面的放置位置时,间隔通过 $\large label \times (w^Tx + b)$ 来计算,这时就能体现出 $-1$ 和 $+1$ 类的好处了。如果数据点处于正方向(即+1类)并且离分隔超平面很远的位置时,$\large w^Tx + b$ 会是一个很大的正数,同时 $\large label \times (w^Tx + b)$ 也会是一个很大的正数。而如果数据点处于负方向($-1$类)并且离分隔超平面很远的位置时,此时由于类别标签为 $-1$,则 $\large label \times (w^Tx + b)$ 仍然是一个很大的正数。
现在的目标就是找出分类器定义中的 $w$ 和 $b$。为此,我们必须找到具有最小间隔的数据点,而这些数据点也就是前面提到的支持向量。一旦找到具有最小间隔的数据点,我们就需要对该间隔最大化。这就可以写作:
$\Large argmax_{w,b} \begin{Bmatrix} min_{n}(label \times (x^T +b)) \times \frac{1}{||w||} \end{Bmatrix}$
直接求解上述问题相当困难,所以我们将它转换成为另一种更容易求解的形式。首先考察一下上式中大括号内的部分。由于对乘积进行优化是一件很讨厌的事情,因此我们要做的是固定其中一个因子而最大化其他因子。如果令所有支持向量的 $label \times (x^T +b)$ 都为 1,那么就可以通过求 $||w||^{-1}$ 的最大值来得到最终解。但是,并非所有数据点的 $label \times (x^T +b)$ 都等于 1,只有那些离分隔超平面最近的点得到的值才为 1。而离超平面越远的数据点,其 $label \times (x^T +b)$ 的值也就越大。
在上述优化问题中,给定了一些约束条件然后求最优值,因此该问题是一个带约束条件的优化问题。这里的约束条件就是 $label \times (x^T +b) \geq 1.0 $。对于这类优化问题,有一个非常著名的求解方法,即拉格朗日乘子法(拉格朗日数乘法)。
剩下具体内容推理及其繁杂,可以参考 1小时候教会你svm支持向量机,学不会来打我!! 当然你如果希望更加清晰的了解,参考这位数学博士的讲解 【合集·支持向量机】 十分钟 机器学习系列 第八篇章:支持向量机
核函数
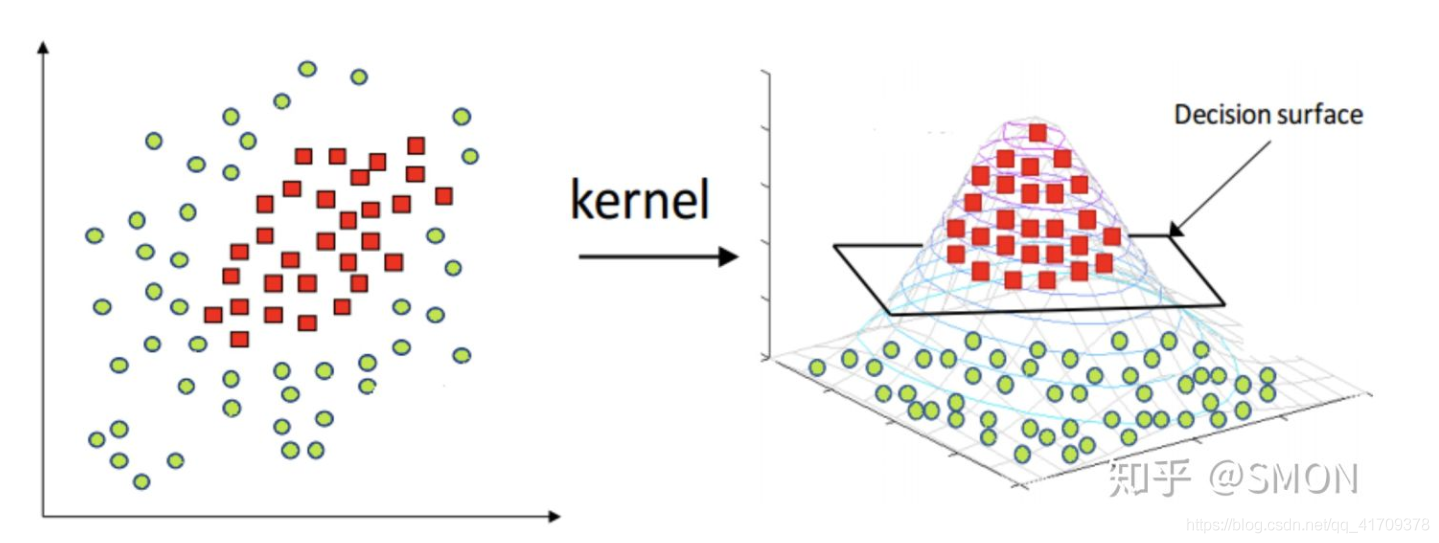
图片来自于知乎:SMON
如上图所示,数据点处于一个圆中,人类的大脑能够意识到这一点。然而,对于分类器而言,它只能识别分类器的结果是大于0 还是 小于 0 。如果只是在 x 和 y 轴构成的坐标系中插入直线进行分类的话,我们并不会得到理想的结果。我们或许可以对圆中的数据进行某种形式的转换,从而得到某些新的变量来表示数据。在这种表示情况下,我们就更容易得到大于 0 或者小于 0 的测试结果。在这个例子中,我们将数据从一个特征空间转换到另一个特征空间。在新空间下,我们可以很容易利用已有的工具对数据进行处理。数学家们喜欢将这个过程称之为从一个特征空间到另一个特征空间的映射。在通常情况下,这种映射会将低维特征空间映射到高维空间。
这种从某个特征空间到另一个特征空间的映射是通过核函数来实现的。你可以把核函数想象成一个包装器(wrapper)或者是接口(interface),它能把数据从某个很难处理的形式转换成为另一个较容易处理的形式。如果上述特征空间映射的说法听起来很让人迷糊的话,那么可以将它想象成为另外一种距离计算的方法。前面我们提到过距离计算的方法。距离计算的方法有很多种,不久我们也将看到,核函数一样具有多种类型。经过空间转换之后,我们可以在高维空间中解决线性问题,这也就等价于在低维空间中解决非线性问题。
SVM优化中一个特别好的地方就是,所有的运算都可以写成内积(inner product,也称点积)的形式。向量的内积指的是两个向量相乘,之后得到单个标量或者数值。我们可以把内积运算替换成核函数,而不必做简化处理。将内积替换成核函数的方式被称为核技巧(kernel trick)或者核“变电”(kernel substation)。
核函数并不仅仅应用于支持向量机,很多其他的机器学习算法也都用到核函数。
End
支持向量机非常好用,但是原理又有一定的复杂性,本来打算弄个例子,目前来看,难度太大,遂决定在后面出使用 scikit-learn 的时候再弄例子。

- 1.健壮"通常指的是系统、软件或算法具有强大、稳定和鲁棒的性能,能够在各种不同的情况下正常运行,即使面对异常或错误输入也能保持良好的表现。 ↩